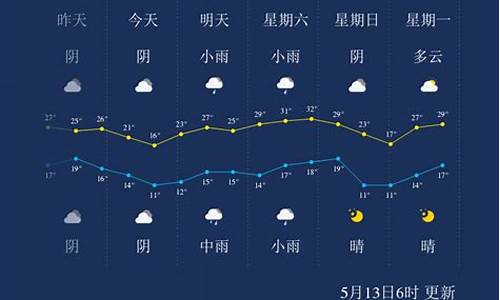
江西省宜春市宜丰县天气预报15天查询_讧酉宜丰天气预报

1.求上海初二数学期中考试卷（一次函数，无理方程，分式方程，高次方程，平行四边形，矩形，正方形，菱形）

2.人教版初二数学下册的期中或期末的试卷

3.中国最适合居住的城市都有哪些？

求上海初二数学期中考试卷（一次函数，无理方程，分式方程，高次方程，平行四边形，矩形，正方形，菱形）

一、填空题（10×3'＝30分）

1、如果反比例函数的图象过点（1、－2），则这个反比例函数的解析式为_______________。

2、分式 的值为0，则X=______________。

3、若 ，则 __________________。

4、化简： _______________。

5、如图1，在四边形ABCD中AB//CD，若加上AD//BC，则四边形ABCD为平行四边形。现在请你添加一个适当的条件：________________________，使得四边形AECF为平行四边形。( 图中不再添加点和线)。

图1 图2

6、如图2，是根据四边形的不稳定性制作的边长为10cm的可活动菱形衣架，若墙上钉子间的距离AB＝BC＝10cm,则∠1＝___________度。

7、如图3,正方形ABCD中,AB=1,点P是对角线AC上一点,分别以AP,PC为对角线作正方形,则两个小正方形的周长的和是_______________.

图3 图4

8、如图4，在梯形ABCD中，AD//CD，对角线AC⊥BD，且AC＝5cm,BD=12cm,则该梯形的两底长之和等于_______________cm.

9、直线Y=2X-1与X轴交于点A，与Y轴交于点B，则AB的长是____________。

如图5，P是反比例函数图象在第一象限的 点，且矩形PEOF的面积为3，则反比例函数表达式为__________________

Y

P

E

O F X

图5

10、直线Y＝2X－4与X轴交于点A，与Y轴交于点B，则AB的长是

二、选择题（本大题共8小题，每小题3分，共24分。第小题只有一个正确选项，把正确选项的代号填入题后括号内。）

11、分式 有意义，则x的取值范围是（ ）

A、X>3 B、X<3 C、X≠3 D、X≠-3

12、天气预报报道宜春市今天最高气温34℃，最低气温20℃，则今天宜春市气温的极差是（ ）

A、54℃ B、14℃ C、－14℃ D、－62℃

13、下列四个函数中，当X>0时，Y随X的增大而增大的是（ ）

A、Y＝ B、Y＝－ C、Y＝－x D、Y＝－2x－1

14、10名学生分虽购买如下尺码的鞋子：20，20，21，22，22，22，23，23，24.（单位：Cm),这组数据中鞋店老板最关心的是（ ）

A、平均数 B、中位数 C、众数 D、方差

15、如图6，正比例函数Y＝X与反比例函数Y＝ 的图象相交于点A、C，AB┴X轴于B，CD┴X轴于D，这四边形ABCD的面积为（ ）

A、1 B、2 C、 D、 A D

A

D

C B 图6 B E C 图7

16、如图7，等腰梯形ABCD中，AD//BC，AE//DC，∠B＝60°，BC＝3，ΔABE的周长为6，则等腰梯形ABCD的周长是（ ）

A、 8 B、 10 C、 12 D、16

17、将一张矩形纸片ABCD如图8那样折起，使顶点C落在C'处，其中AB＝4，若∠C'ED＝30°，则折痕ED的长为（ ）

A C'

A、4 B、 C、 D、8 D

B

E C

18、如图9，在同一直角坐标系中，正比例函数y＝kx+3与反比例函数y= 的图象位置可能是（ ）

y y y y

x x

x

A B C D

三、（本大题共3小题，第19题，第20题各4分，第21题5分，共13分）

19、化简：

20、解方程：

21、先化简，再选择你喜欢的又使原式有意义的一个x的值代入求值。

四、（本大题共3小题，每小题各6分，共18分）

22、宜丰县蔬菜大户老李有一块正方形菜地，他准备在菜地中间空出两条笔直的交叉的小路，把菜地平均分成面积相等的四部分进行特色种植。请你在下图中添加两条相交线，帮助老李设计三种不同的分割方案，并简要说明作图方法。

方法一 方法二 方法三

23、如图10，已知 ABCD中，E为AD中点，CE的延长线交BA延长线于点F。求证：A 是BF的中点

C D

E

B F

A

如图10

24、张老师要从班级里数学 成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学 联赛”。为此，他对两位同学进行了辅导，并在辅导期间测验了10次，测验成绩如下表：

第1次 2 3 4 5 6 7 8 9 10

甲 68 80 78 79 78 84 81 83 77 92

乙 86 80 75 83 79 80 85 80 77 75

利用表中数据，解答下列问题：（1）填空完成下表：

平均成绩 中位数 众数

甲 80 79.5

乙 80 80

（2）张老师从测验成绩表中，求得甲的方差S甲2 ＝33.2，请你计算乙10次测验成绩的方差。

（3）请你根据上面的信息，运用所学统计知识，帮张老师选拔出参加“全国数学联赛”的人选，并简要说明理由。

五、（本大题共两小题，第25题7分，第26题8分，共15分）

25、如图11，一次函数y=kx+b的图象与反比例函数y= 的图象交于A、B两点。

（1）利用图中条件，求反比例函数的解析式及n的值。

y

A（－2，1）

x

B（1，n)

图11

（2）求一次函数的解析式。

（3）根据图象写出使一次函数的值大于反比例函数值的x的取值范围。

26、如图12，菱形ABCD的边CD在菱形ECGF的边CE上，且D是CE中点。连接BE，DF。

（1）观察猜想BE与DF之间的大小关系，并证明你的结论。

（2）图中是否存在旋转能够 互相重合的两个三角形？若存在，请说明旋转过程：若不存在，请说明理由。

回答者： 鬼剑士杰 - 见习魔法师 3-21 22:36

一、填空题：（每空2分，共32分）

1．计算： __________。

2．16的平方根是__________。

3． 的绝对值是__________。

4．在实数范围内分解因式： __________。

5．函数 中，自变量x的取值范围是__________。

6．若直线 与直线 平行，那么 的解析式为__________。

7．反比例函数过点P（2，3），则此函数解析式为__________。

8．写出一个不经过第三象限的一次函数解析式__________。

9．等腰三角形，腰长为x，底为y，周长为30，则y与x的函数关系式为__________，自变量x的取值范围是__________。

10．若 ，则 __________。

11．若 ，则 __________。

12．如图，△ABC中，点D、E分别在AB、AC上。

（1）如果DE‖BC，且AD＝5cm，BD＝3cm，AE＝4cm，那么CE＝________cm。

（2）如果AD＝3cm，DB＝2cm，AC＝4cm，要使DE‖BC，那么AE＝__________ cm。

13．梯形的上、下底的差为6，中位线长为5，则上底、下底各为__________。

14．若 ，则 的算术平方根为__________。

二、选择题：（每题2分，共14分）

15．在 这五个实数中是无理数的有（ ）

A．1个 B．2个 C．3个 D．4个

16．若 ，则 等于（ ）

A． B． C． D．

17．下列各组中的四条线段是成比例线段的是（ ）

A．

B．

C．

D．

18．如图，CD‖AB，下列各式中错误的是（ ）

A． B．

C． D．

19．如果点 与点 关于y轴对称，那么 的值为（ ）

A．1 B．－1 C．7 D．－7

20．已知 ，则函数 的图象大致是（ ）

21．已知函数：（1） ；（2） ；（3） ，其中y随x的增大而增大的函数有（ ）

A．0个 B．1个 C．2个 D．3个

三、解答题：

26．汽车行驶时，油箱中有油4升，若每小时耗油0.5升，求油箱中剩余油量y（升）与工作时间t（小时）间的函数关系式及自变量t的取值范围，并画出此函数的图象。（5分）

27．如图， 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。

（1）B出发时与A相距___________千米。

（2）走了一段路后，自行车发生故障，进行修理，所用的时间是___________小时。

（3）B出发后___________小时与A相遇。

（4）若B的自行车不发生故障，保持出发时的速度前进，___________小时与A相遇，相遇点离B的出发点___________千米。（7分）

28．直线 分别与x轴、y轴交于A、B两点。

（1）在直角坐标系中画出函数图象；

（2）求出直线 与两坐标轴围成的三角形的面积；

（3）做出直线 关于x轴对称的直线 ，并求出直线 的解析式。（8分）

29．如图，D、E、F分别是△ABC各边的中点。

（1）若 ，则BC＝__________cm，若AB＝10cm，则DF＝__________cm。

（2）中线AD与中位线EF有什么特殊关系？

答：______________________________；

（3）若增加条件AB＝AC，则四边形AEDF是什么四边形？

答：______________________________；

（4）若增加条件AB＝AC，且∠BAC＝90°，则四边形AEDF是什么四边形？

答：______________________________；

（5）证明第二问的结论。（8分）

30．如图，在△ABC中，∠1＝∠2，CE‖AD交BA延长线于E。

求证： （5分）

31．已知：在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，AC＝4cm，AB边上有一只小虫P，由A向B沿AB以1cm/秒的速度爬行，过P做PE⊥BC于E，PF⊥AC于F，求：

（1）矩形PECF的周长y（cm）与爬行时间t（秒）的函数关系式，及自变量的取值范围；

（2）小虫爬行多长时间，四边形PECF是正方形。（5分）

四、选做题：（普通班选做，实验班必做）

32．在平面直角坐标系内，一次函数 的图像分别与x轴、y轴和直线 交于点A、B、C，直线 与x轴交于点D，四边形OBCD（O是坐标原点）的面积是10，若点A的横坐标是 ，求这个一次函数的解析式。（10分）

33．已知：如图，点D在AB上，点E在BC延长线上，AD＝CE。

求证： （10分）

人教版初二数学下册的期中或期末的试卷

一、填空题（10×3'＝30分）

1、如果反比例函数的图象过点（1、－2），则这个反比例函数的解析式为_______________。

2、分式 的值为0，则X=______________。

3、若 ，则 __________________。

4、化简： _______________。

5、如图1，在四边形ABCD中AB//CD，若加上AD//BC，则四边形ABCD为平行四边形。现在请你添加一个适当的条件：________________________，使得四边形AECF为平行四边形。( 图中不再添加点和线)。

图1 图2

6、如图2，是根据四边形的不稳定性制作的边长为10cm的可活动菱形衣架，若墙上钉子间的距离AB＝BC＝10cm,则∠1＝___________度。

7、如图3,正方形ABCD中,AB=1,点P是对角线AC上一点,分别以AP,PC为对角线作正方形,则两个小正方形的周长的和是_______________.

图3 图4

8、如图4，在梯形ABCD中，AD//CD，对角线AC⊥BD，且AC＝5cm,BD=12cm,则该梯形的两底长之和等于_______________cm.

9、直线Y=2X-1与X轴交于点A，与Y轴交于点B，则AB的长是____________。

如图5，P是反比例函数图象在第一象限的 点，且矩形PEOF的面积为3，则反比例函数表达式为__________________

Y

P

E

O F X

图5

10、直线Y＝2X－4与X轴交于点A，与Y轴交于点B，则AB的长是

二、选择题（本大题共8小题，每小题3分，共24分。第小题只有一个正确选项，把正确选项的代号填入题后括号内。）

11、分式 有意义，则x的取值范围是（ ）

A、X>3 B、X<3 C、X≠3 D、X≠-3

12、天气预报报道宜春市今天最高气温34℃，最低气温20℃，则今天宜春市气温的极差是（ ）

A、54℃ B、14℃ C、－14℃ D、－62℃

13、下列四个函数中，当X>0时，Y随X的增大而增大的是（ ）

A、Y＝ B、Y＝－ C、Y＝－x D、Y＝－2x－1

14、10名学生分虽购买如下尺码的鞋子：20，20，21，22，22，22，23，23，24.（单位：Cm),这组数据中鞋店老板最关心的是（ ）

A、平均数 B、中位数 C、众数 D、方差

15、如图6，正比例函数Y＝X与反比例函数Y＝ 的图象相交于点A、C，AB┴X轴于B，CD┴X轴于D，这四边形ABCD的面积为（ ）

A、1 B、2 C、 D、 A D

A

D

C B 图6 B E C 图7

16、如图7，等腰梯形ABCD中，AD//BC，AE//DC，∠B＝60°，BC＝3，ΔABE的周长为6，则等腰梯形ABCD的周长是（ ）

A、 8 B、 10 C、 12 D、16

17、将一张矩形纸片ABCD如图8那样折起，使顶点C落在C'处，其中AB＝4，若∠C'ED＝30°，则折痕ED的长为（ ）

A C'

A、4 B、 C、 D、8 D

B

E C

18、如图9，在同一直角坐标系中，正比例函数y＝kx+3与反比例函数y= 的图象位置可能是（ ）

y y y y

x x

x

A B C D

三、（本大题共3小题，第19题，第20题各4分，第21题5分，共13分）

19、化简：

20、解方程：

21、先化简，再选择你喜欢的又使原式有意义的一个x的值代入求值。

四、（本大题共3小题，每小题各6分，共18分）

22、宜丰县蔬菜大户老李有一块正方形菜地，他准备在菜地中间空出两条笔直的交叉的小路，把菜地平均分成面积相等的四部分进行特色种植。请你在下图中添加两条相交线，帮助老李设计三种不同的分割方案，并简要说明作图方法。

方法一 方法二 方法三

23、如图10，已知 ABCD中，E为AD中点，CE的延长线交BA延长线于点F。求证：A 是BF的中点

C D

E

B F

A

如图10

24、张老师要从班级里数学 成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学 联赛”。为此，他对两位同学进行了辅导，并在辅导期间测验了10次，测验成绩如下表：

第1次 2 3 4 5 6 7 8 9 10

甲 68 80 78 79 78 84 81 83 77 92

乙 86 80 75 83 79 80 85 80 77 75

利用表中数据，解答下列问题：（1）填空完成下表：

平均成绩 中位数 众数

甲 80 79.5

乙 80 80

（2）张老师从测验成绩表中，求得甲的方差S甲2 ＝33.2，请你计算乙10次测验成绩的方差。

（3）请你根据上面的信息，运用所学统计知识，帮张老师选拔出参加“全国数学联赛”的人选，并简要说明理由。

五、（本大题共两小题，第25题7分，第26题8分，共15分）

25、如图11，一次函数y=kx+b的图象与反比例函数y= 的图象交于A、B两点。

（1）利用图中条件，求反比例函数的解析式及n的值。

y

A（－2，1）

x

B（1，n)

图11

（2）求一次函数的解析式。

（3）根据图象写出使一次函数的值大于反比例函数值的x的取值范围。

26、如图12，菱形ABCD的边CD在菱形ECGF的边CE上，且D是CE中点。连接BE，DF。

（1）观察猜想BE与DF之间的大小关系，并证明你的结论。

（2）图中是否存在旋转能够 互相重合的两个三角形？若存在，请说明旋转过程：若不存在，请说明理由。

回答者： 鬼剑士杰 - 见习魔法师 3-21 22:36

一、填空题：（每空2分，共32分）

1．计算： __________。

2．16的平方根是__________。

3． 的绝对值是__________。

4．在实数范围内分解因式： __________。

5．函数 中，自变量x的取值范围是__________。

6．若直线 与直线 平行，那么 的解析式为__________。

7．反比例函数过点P（2，3），则此函数解析式为__________。

8．写出一个不经过第三象限的一次函数解析式__________。

9．等腰三角形，腰长为x，底为y，周长为30，则y与x的函数关系式为__________，自变量x的取值范围是__________。

10．若 ，则 __________。

11．若 ，则 __________。

12．如图，△ABC中，点D、E分别在AB、AC上。

（1）如果DE‖BC，且AD＝5cm，BD＝3cm，AE＝4cm，那么CE＝________cm。

（2）如果AD＝3cm，DB＝2cm，AC＝4cm，要使DE‖BC，那么AE＝__________ cm。

13．梯形的上、下底的差为6，中位线长为5，则上底、下底各为__________。

14．若 ，则 的算术平方根为__________。

二、选择题：（每题2分，共14分）

15．在 这五个实数中是无理数的有（ ）

A．1个 B．2个 C．3个 D．4个

16．若 ，则 等于（ ）

A． B． C． D．

17．下列各组中的四条线段是成比例线段的是（ ）

A．

B．

C．

D．

18．如图，CD‖AB，下列各式中错误的是（ ）

A． B．

C． D．

19．如果点 与点 关于y轴对称，那么 的值为（ ）

A．1 B．－1 C．7 D．－7

20．已知 ，则函数 的图象大致是（ ）

21．已知函数：（1） ；（2） ；（3） ，其中y随x的增大而增大的函数有（ ）

A．0个 B．1个 C．2个 D．3个

三、解答题：

26．汽车行驶时，油箱中有油4升，若每小时耗油0.5升，求油箱中剩余油量y（升）与工作时间t（小时）间的函数关系式及自变量t的取值范围，并画出此函数的图象。（5分）

27．如图， 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。

（1）B出发时与A相距___________千米。

（2）走了一段路后，自行车发生故障，进行修理，所用的时间是___________小时。

（3）B出发后___________小时与A相遇。

（4）若B的自行车不发生故障，保持出发时的速度前进，___________小时与A相遇，相遇点离B的出发点___________千米。（7分）

28．直线 分别与x轴、y轴交于A、B两点。

（1）在直角坐标系中画出函数图象；

（2）求出直线 与两坐标轴围成的三角形的面积；

（3）做出直线 关于x轴对称的直线 ，并求出直线 的解析式。（8分）

29．如图，D、E、F分别是△ABC各边的中点。

（1）若 ，则BC＝__________cm，若AB＝10cm，则DF＝__________cm。

（2）中线AD与中位线EF有什么特殊关系？

答：______________________________；

（3）若增加条件AB＝AC，则四边形AEDF是什么四边形？

答：______________________________；

（4）若增加条件AB＝AC，且∠BAC＝90°，则四边形AEDF是什么四边形？

答：______________________________；

（5）证明第二问的结论。（8分）

30．如图，在△ABC中，∠1＝∠2，CE‖AD交BA延长线于E。

求证： （5分）

31．已知：在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，AC＝4cm，AB边上有一只小虫P，由A向B沿AB以1cm/秒的速度爬行，过P做PE⊥BC于E，PF⊥AC于F，求：

（1）矩形PECF的周长y（cm）与爬行时间t（秒）的函数关系式，及自变量的取值范围；

（2）小虫爬行多长时间，四边形PECF是正方形。（5分）

四、选做题：（普通班选做，实验班必做）

32．在平面直角坐标系内，一次函数 的图像分别与x轴、y轴和直线 交于点A、B、C，直线 与x轴交于点D，四边形OBCD（O是坐标原点）的面积是10，若点A的横坐标是 ，求这个一次函数的解析式。（10分）

33．已知：如图，点D在AB上，点E在BC延长线上，AD＝CE。

求证： （10分）

中国最适合居住的城市都有哪些？

中国最适合居住的城市：三亚、厦门、昆明

三亚

三亚是具有热带海滨风景特色的国际旅游城市，又被称为“东方夏威夷”。

三亚市区三面环山，北有抱坡岭，东有大会岭、虎豹岭和海拔393米的高岭（狗岭），南有南边岭，形成环抱之势，山岭绵延起伏、层次分明。

同时，山脉的延伸将市区分成若干青山围成的空间，为城市不同地区提供了各具特色的空间景观环境。三亚面临南海，海湾较多，众多海湾各有佳景。处于市区的大东海、小东海、三亚湾与市民生活的关系最为密切。

厦门

隶属于福建省，别称鹭岛， 简称厦、鹭，?副省级城市、经济特区，东南沿海重要的中心城市、港口及风景旅游城市。厦门位于福建省东南端，东与大小金门岛、南与龙海市隔海相望，陆地与南安市、安溪县、长泰县、龙海市接壤。

厦门由本岛厦门本岛、离岛鼓浪屿、西岸海沧半岛、北岸集美半岛、东岸翔安半岛、大小嶝岛、内陆同安、九龙江等组成，陆地面积1699.39平方公里，海域面积390多平方公里。厦门通行闽南方言，是闽南地区的主要城市，与漳州、泉州并称厦漳泉闽南金三角经济区。

昆明

昆明开放而时尚，浓缩了云南的区位优势，从两千多年前的“南方丝绸之路”到开放的昆明一直是东亚大陆与中南半岛、南亚次大陆各国进行经济贸易往来及政治联系的陆路枢纽。“中国昆明进出口商品交易会”、“中国国际旅游交易会”、“中国昆明国际旅游节”使昆明成为中国主要的会展城市之一。

昆明三面环山，南濒滇池，滇池是云南省最大的高原湖泊，全国第六大淡水湖泊，沿湖两岸风光绮丽。由于地处低纬高原而形成“四季如春”的气候，特别是有高原湖泊滇池在调节着温湿度，使这里空气清新、天高云淡、阳光明媚、鲜花常开。